Das Geheimnis der Trägheitsbewegung
Studie
Der Vektorraum ist eine unterstützende Umgebung für die Bewegung
von Körpern.
Körper und Strukturen mit Vektoreigenschaften werden im Vektorraum
fixiert.
Die Realisierung eines spezifischen räumlichen Antriebssystems ist
nur möglich,
wenn die Wechselwirkungen von Körpern mit dem Vektorraum bekannt
sind.
Beispiele: Um einen Körper im Vektorraum zu bewegen, ist eine
Kraft
erforderlich, dann bewegt sich der Körper träge in die durch
die Kraft
vorgegebene Richtung. Trägheitsbewegung ist eine Wechselwirkung des
Vektorkörpers mit dem Vektorraum. Die Bewegung des Körpers richtet
die
räumlichen Vektorpolaritäten parallel zur Bewegungsrichtung
aus. Die parallelen
Polarisationen stoßen sich radial ab und bilden geschlossene orthogonale,
elektromagnetische Vektorkreise um den Körper. Somit erzeugt die
Bewegung des Körpers im ihn umgebenden Raum ein elektromagnetisches
Vehikel, vereint mit der Körperbewegung. Im Bewegungspfad dieses
Wellenträgers öffnen sich die parallelen Polarisationen radial
und schließen
sich nach hinten, wie man in der Antike glaubte. Die Welle, die Schwingungen
der Orientierung der Polaritäten sind also die Trägheitsbewegung.
In der Atmosphäre entstehen durch die Bewegung von Luftströmungen
solche „Fahrzeuge“, sogenannte Zyklone oder Hurrikane, die das
Phänomen
veranschaulichen. Die „greifbarsten“ Beispiele sind der Straßenverkehr
in
Kurven, wo die Kraft, die die Richtung ändert, Trägheit in „Zentrifugalkraft“
umwandelt. Daher ist Trägheitsbewegung keine „Eigenschaft von
Körpern“, sondern
Wechselwirkungen von Vektoreigenschaften undEnergie. Trägheitsbewegung
ist ein elektromagnetisches Phänomen, wie das von den Perseiden erzeugte
„Feuer“.
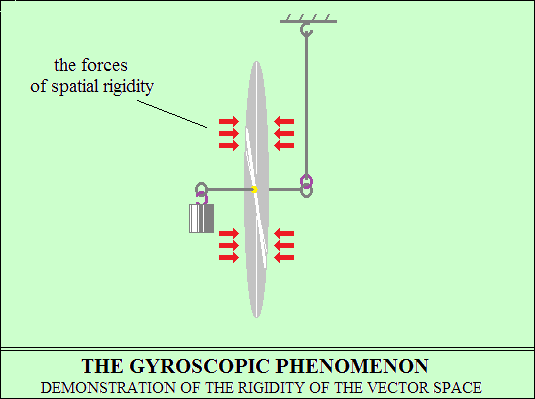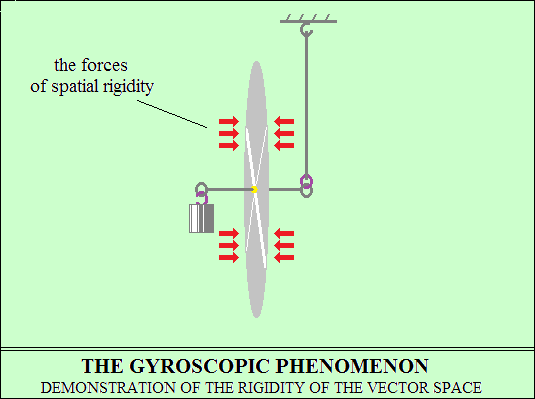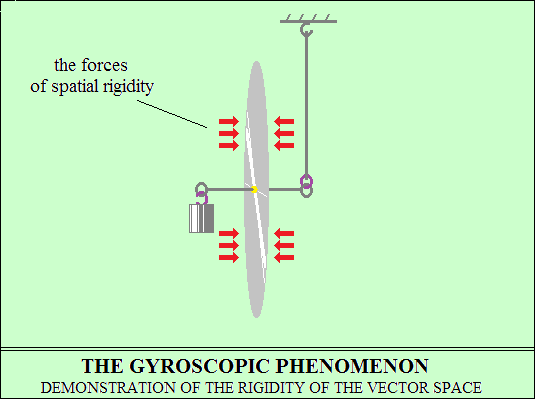
Trägheitsbewegung der Rotation – das Gyroskop.
Um eine Scheibe um ihre Mittelachse zu drehen, ist ein Drehimpuls erforderlich,
dann dreht sich die Scheibe träge. Trägheitsrotation ist die
Wechselwirkung
der Vektorscheibe mit dem Vektorraum. Durch die Rotation der Scheibe
werden die Polaritäten der Raumvektoren auf den Oberflächen
der Scheibe
in die gleiche Richtung ausgerichtet, wodurch abstoßende Kräfte
erzeugt werden.
Die Rotation der Scheibe, die zwischen zwei Oberflächen mit Abstoßungskräften
gefangen ist, kann die Rotationsebene nicht verlassen, da die Abstoßungskräfte
Starrheit aufweisen, wie das Experiment zeigt. Die Abstoßungskräfte
ermöglichen die Bewegung der Scheibe nur in der Rotationsebene,
begleitet von der Steifigkeit der durch ihre Rotation erzeugten Kräfte.
Resultierende Daten
Um ein für den Vektorraum spezifisches Antriebssystem zu schaffen,
kann es
sich um die Steifigkeit der durch die Rotation erzeugten Kräfte und
allgemein
um die elektrostatischen oder elektromagnetischen Abstoßungskräfte
handeln.