Configuration relativement
statique.
La configuration de l'espace vectoriel de l'atmosphère terrestre,
orientée
par la densité du champ magnétique polaire, semble relativement
statique.
Le noyau ne comprime et n'aligne qu'un segment du circuit du champ
magnétique, formant l'axe magnétique. Les forces répulsives
du champ
magnétique, libres de compression, se relâchent autour de
l'axe comprimé,
jusqu'à être équilibrées par les forces attractives.
Dans cet état apparemment
statique, les forces attractives augmentent la densité de l'espace
vectoriel
orienté, maximale sur l'axe magnétique. Ainsi, une hiérarchie
statique de la
densité de l'espace vectoriel orienté est établie,
configuration caractéristique
des structures vectorielles macroscopiques. Dans cette configuration,
l'espace vectoriel orienté ne se déplace pas vers le centre,
mais se compose
de structures vectorielles, statiques ou dynamiques. De telles interactions
ont été interprétées par Aristote, Archimède
et d'autres. Aristote a expliqué
pourquoi certains corps tombent et d'autres montent vers le ciel, et
Archimède a expliqué pourquoi certains corps coulent dans
l'eau et d'autres
flottent. Personne ne dit pourquoi les avions peuvent voler. De toute
évidence, la configuration de l'espace vectoriel, étant
récente, est absente
de la culture de la civilisation. Dans la culture de la civilisation,
on
considère que la Terre a été créée
par Dieu, ou, comme le disait
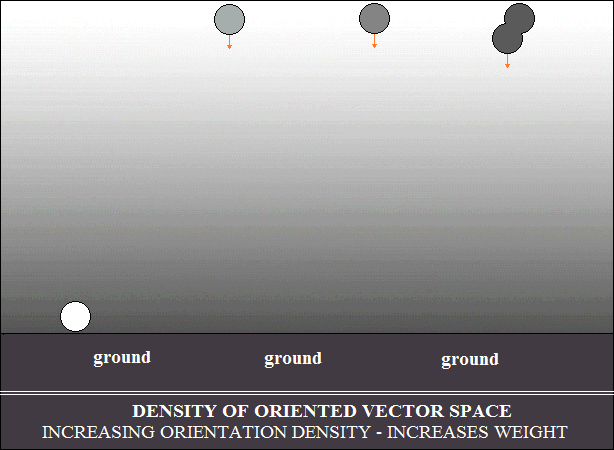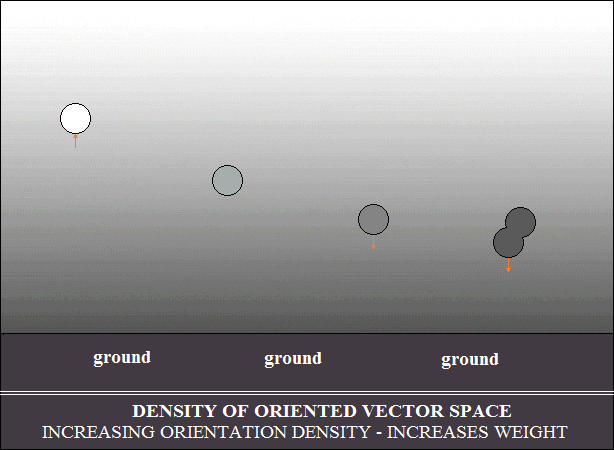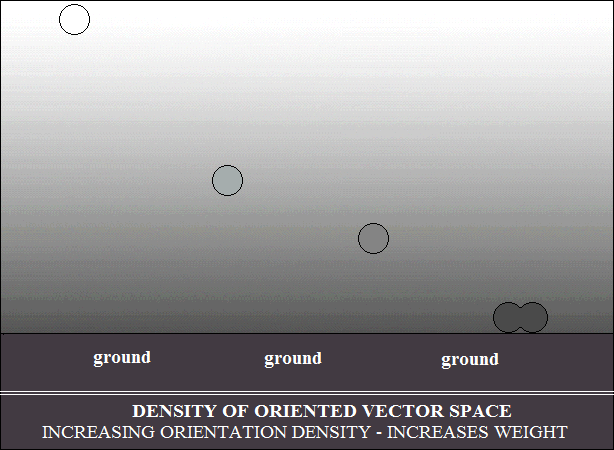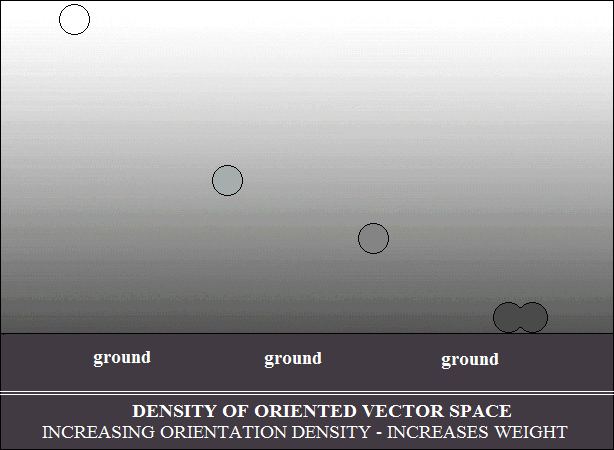
Georges Lemaitre, par le Big Bang. Le premier schéma montre comment
la
densité d'orientation de l'espace vectoriel justifie le raisonnement
d'Aristote
et la loi d'Archimède. Le deuxième schéma illustre
la composition
vectorielle de la vitesse de mouvement des objets, avec la densité
d'orientation de l'espace vectoriel dans lequel ils se déplacent.
La vitesse de mouvement oriente l'espace vectoriel dans la direction
et le sens du mouvement. L'orientation étant parallèle,
les forces répulsives
réduisent la densité d'orientation de l'espace vectoriel.
L'objet est ainsi