Wechselwirkungen
im Vektorraum.
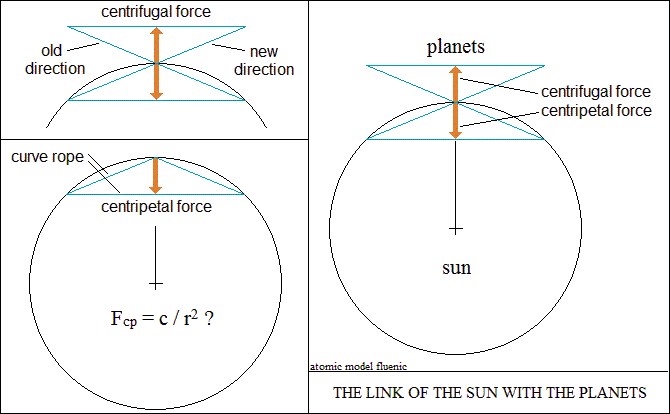
Die Zentripetal- und Zentrifugalkräfte werden "im Spiegel"
durch dasselbe Phänomen durch die Richtungseigenschaft der Vektoren erzeugt.
Die maximale Anziehungskraft richtet die Vektoren kollinear in die gleiche
Richtung.
Zentripetalkraft
In rein vektorisierten geschlossenen Schaltkreisen, die als elektrisch
und magnetisch bezeichnet werden, wandelt diese Eigenschaft den
Kurvenbogen in einer geraden Linie in eine Zeichenfolge um.
Auf diese Weise wird die Schaltung mit Lichtgeschwindigkeit zur Mitte komprimiert.
Die Anziehungskraft zwischen den Vektoren wird nun in die Zentripetalkraft
umgewandelt.
Zentrifugalkraft
Die Zentrifugalkraft ist die Reaktion des Vektorraums auf die Bewegung des
Körpers (offener Kreislauf).
Die lineare Bewegung richtet Raumvektoren in die gleiche Richtung
aus, ein Phänomen, das als Trägheit bezeichnet wird.
Das Ändern der Bewegungsrichtung ändert auch die Richtung
der Ausrichtung von räumlichen Vektoren.
Die zwei Vektorrichtungen, die die Kurve tangieren, bilden zwei "im Spiegel"
-Winkel.
Wie bei geschlossenen Kreisläufen werden die Winkel
zu gleichen Saiten und Kräften mit entgegengesetzten Richtungen.
Das äußere Seil repräsentiert die Zentrifugalkraft.
Das innere Seil repräsentiert die Zentripetalkraft, die die Bewegung
des Körpers krümmt.
Die Interpretation zeigt den engen Zusammenhang zwischen Zentripetalkraft
und Zentrifugalkraft.
Aus Experimenten hängt die Zentrifugalkraft von der Geschwindigkeit
des Körpers und dem Winkel der beiden Tangenten bzw. vom Krümmungsradius
ab.
Die Zentrifugalkraft ist also proportional zur Geschwindigkeit
und umgekehrt proportional zum Radius Fcf = v / r
Im Fall der Zentripetalkraft, wobei die Geschwindigkeit der Vektoranziehung
die Lichtgeschwindigkeit ist, wird das Gesetz der universellen Anziehung:
Fcp = c / r2