Vektorraum.
Die Besonderheit des Vektorraums ist die Empfindlichkeit der
Vektorpolaritäten, sofort zu interagieren, wie die Touch-Funktion von
Mobiltelefonen, die nur wenige, sehr wenige Benutzer verstehen.
Die Interaktionen der Vektoreigenschaften sind die grundlegende Form der
Energie. Sehr wichtig sind die Diskussionen auf Wikipedia bezüglich der
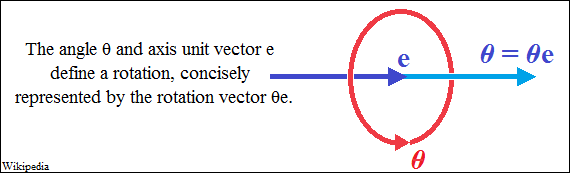
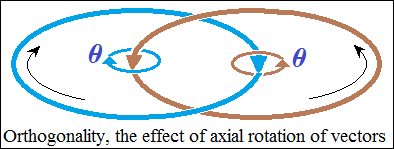
axialen Rotation der Vektoren nach rechts (siehe Zeichnung). Die axiale
Rotation von Vektoren ist eine bisher unbekannte Vektoreigenschaft, die
Ursache für die Struktur orthogonal geschlossener Kreise (siehe Zeichnung).
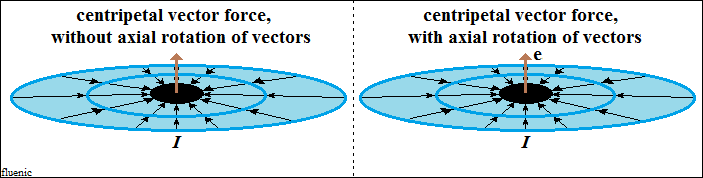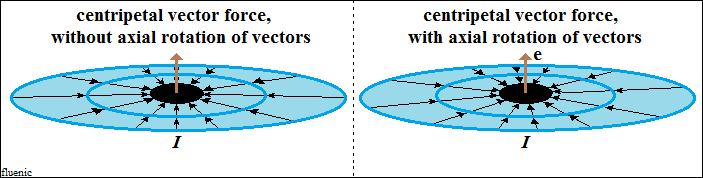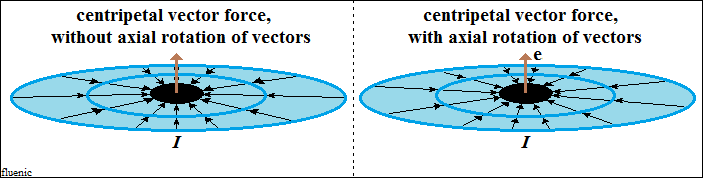
Der Modul eines Vektors in einem geschlossenen Kreis nimmt plötzlich gegen
Null ab, wodurch die Zentripetalkraft erzeugt wird. Die Zentripetalkräfte der
orthogonal geschlossenen Kreise komprimieren ihre Dichte gegenseitig und
bilden eine Vektorstruktur, die als Wasserstoffkern bezeichnet wird.
Die einzige dimensionale Grenze des Vektorraums ist die Dichte der
Vektorpolaritäten, die in den orthogonal geschlossenen Kreisen im
Wasserstoffkern ausgerichtet sind. Die potentielle Energie von Wasserstoff
ist spezifisch und wird durch die maximal mögliche Dichte orthogonal
geschlossener symmetrischer Vektorkreise bestimmt. Der Wasserstoffkern ist
kein Atom, also unzerstörbar, er rotiert nicht, da die Rotationsebene der
Kreise orthogonal ist, heben sie sich gegenseitig auf. Die orthogonalen Kreise
des Wasserstoffs sind symmetrisch, er hat keinen Magnetismus, er hat keine
Elektrizität, jeder Kreis hat offene Vektorpolaritäten, ist also tetrapolar.
Der Kern, die potentielle Energie, ist in orthogonal geschlossenen Kreisen
komprimierter Vektorraum, der in kinetische Energie, in Schwingungen des
Vektorraums, in Licht umgewandelt werden kann. Die Umwandlung des
Wasserstoffs kann in der Aktivität der Sonne „abgelesen“ werden.
Der Druck der zentripetalen Vektorkraft in der Gassphäre steigt exponentiell an.
In der unteren Atmosphäre der Sonne erzeugt der Druck die erste Phase der
Umwandlung der potentiellen Energie des Wasserstoffs in kinetische Energie,
wodurch die Chromosphäre entsteht. In der Chromosphäre überwiegen die
Fusions- und Vervielfältigungsreaktionen des Wasserstoffs. Der zunehmende
Druck drückt den vermehrten Wasserstoff in die nächste Phase, die
Photosphäre, wo potentielle Energie in kinetische Energie umgewandelt wird.
In der Photosphäre gleicht kinetische Energie einem „thermischen Inferno“,
der Wasserstoff wird in kontinuierlich radial und zentripetal ausgestoßene
Schwingungen zerlegt. Während die radiale Emission von Schwingungen gut
bekannt ist, ist die interne Emission von Schwingungen völlig unbekannt.
Die Wellenlänge der zentripetal ausgestoßenen Schwingungen steigt
proportional zum Druck, der exponentiell ansteigt, und die intern
ausgestoßenen Schwingungen werden zu Komponenten der orthogonalen
solaren Kreise. Unbekannt ist der Zustand des Vektorraums im Inneren über
einen Radius von Hunderttausenden von Kilometern. Rational betrachtet ist das
Innere der Sonne mit orthogonal geschlossenen Vektorkreisen gefüllt, wobei die
Dichte des Vektorraums zum Zentrum hin exponentiell zunimmt. Die Variation
der Dichte des Vektorraums erreicht also das Zentrum im festen Zustand.
Die Bewegung von Körpern im Universum.
Mikroskopische und makroskopische Vektorstrukturen sind Vektorräume
mit unterschiedlichen Orientierungsdichten in Richtung und Richtung, die als
Formen, Körper, Materie bezeichnet werden. Offensichtlich sind diese
Strukturen nicht unabhängig und durch den Vektorraum begrenzt.
Körper bleiben mit offenen Polaritäten im Vektorraum, wo sie erzeugt
wurden, fixiert. Die Anordnung der Körper im Vektorraum wird durch ihre
radialen Polarisationen mit gleichem Vorzeichen bewahrt, die sich gegenseitig
abstoßen und eine Expansion erzeugen. Die Bewegung galaktischer Systeme
im Vektorraum ist also eine Expansion. In makroskopischen, asymmetrischen
Strukturen, in Planeten-, Stern- und galaktischen Systemen nimmt die potentielle
Energie des „Kerns“ zu, abhängig von der Zugabe von Wasserstoffgas.
Das gemeinsame Merkmal asymmetrischer Strukturen ist der zentripetale
Vektordruck mit exponentiellem Wachstum und die differentielle
Rotationsbewegung. Die differentielle Rotationsbewegung ist durch den
Kreiseleffekt eine weitere Art der Stabilität. Diese Phänomene erfordern klare
Erklärungen der Wechselwirkung von Vektoreigenschaften. Beispielsweise
wird im Sonnensystem der exponentielle Druckanstieg durch die
Zentripetalkräfte orthogonal geschlossener Vektorkreise erzeugt.
- Die differentielle Rotation des Sonnensystems wird durch die axiale
Rotation der Vektoren nach rechts bestimmt. Die orthogonal
geschlossenen Vektorkreise, elektrisch und magnetisch, erzeugen
Zentripetalkräfte und Rotationsbewegungen. Die Ebenen der magnetischen
Kreise stoßen sich um den elektrischen Kreis herum ab und bilden die
magnetische Achse, wodurch der Rotationseffekt aufgehoben wird.
Nur der elektrische Kreis hat eine äquatoriale Rotationsebene mit dem
Mittelpunkt in der magnetischen Achse, die den Magnetismus in Rotation
versetzt. Die axiale Rotation der Vektoren nach rechts bildet das Wesen
der magnetischen Achse. Die enorme Dichte offener Polaritäten in der
magnetischen Achse, die parallel sind, polarisiert den Vektorraum krummlinig
und bidirektional. Am Apogäum des Sonnensystems schließen sich die
krummlinigen Vektorkreise kontinuierlich und nehmen die Zentripetalkraft
wieder auf, wobei die Dichte der Kreise zum Zentrum des Sonnensystems hin
zunimmt. Offensichtlich ist die Zunahme der Dichte der Kreise zum Zentrum
des Systems hin auch die Ursache für die differentielle Rotation, die im
Zentrum maximal ist. Die Planeten des Sonnensystems bewegen sich nicht
auf Umlaufbahnen „im“ Vektorraum, die differentielle Rotationsbewegung ist
die des Sonnensystems, des Vektorraums, in dem sich die Planetensysteme
befinden. Im Sonnensystem oszillieren die Planetensysteme in Richtung des
Sonnenstrahls, zwischen Apogäum und Perigäum, abhängig von der
Variation der Dichte der orthogonalen Sonnenkreise.
Beachten Sie den Ursprung.
Die winzige Vektorenergie wird zur Energie eines Sterns!
Die winzige Vektorrotation wird zur Rotation einer Galaxie!